|
Страница 4 из 4 При решении данной конкретной задачи начнем с уровня , где имеется цель At (Spare, Axle). Единственным вариантом, который может применяться для достижения этого множества целей, является PutOn( Spare, Axle). В результате мы переходим в состояние поиска на уровне , где имеется цель At (Spare, Axle). Единственным вариантом, который может применяться для достижения этого множества целей, является PutOn( Spare, Axle). В результате мы переходим в состояние поиска на уровне 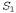 с целями At {Spare, Ground) и с целями At {Spare, Ground) и 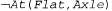 . Первой цели можно достичь только с помощью действия Remove(Spare, Trunk), а последней— с помощью либо Remove{Flat, Axle), либо LeaveOvernight. Но действие LeaveOvernight является взаимно исключающим по отношению к Remove (Spare, Trunk), поэтому единственное решение состоит в том, чтобы выбрать Remove(Spare, Trunk) и Remove (Flat, Axle). В результате мы переходим в состояние поиска на уровне . Первой цели можно достичь только с помощью действия Remove(Spare, Trunk), а последней— с помощью либо Remove{Flat, Axle), либо LeaveOvernight. Но действие LeaveOvernight является взаимно исключающим по отношению к Remove (Spare, Trunk), поэтому единственное решение состоит в том, чтобы выбрать Remove(Spare, Trunk) и Remove (Flat, Axle). В результате мы переходим в состояние поиска на уровне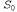 с целями At (Spare, Trunk) и At {Flat, Axle). Обе из этих целей присутствуют в данном состоянии, поэтому налицо готовое решение: действия Remove { Spare, Trunk) и Remove (Flat, Axle) на уровне А0, за которыми следует действие PutOn (Spare, Axle) на уровне с целями At (Spare, Trunk) и At {Flat, Axle). Обе из этих целей присутствуют в данном состоянии, поэтому налицо готовое решение: действия Remove { Spare, Trunk) и Remove (Flat, Axle) на уровне А0, за которыми следует действие PutOn (Spare, Axle) на уровне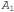 . . Известно, что задача планирования является PSPACE-полной и что для построения графа планирования требуется полиномиальное время, поэтому в наихудшем случае может возникнуть ситуация, в которой извлечение решения окажется неосуществимым. Таким образом, потребуется определенное эвристическое руководство при выборе среди действий в ходе обратного поиска. Одним из подходов, хорошо зарекомендовавших себя на практике, является жадный алгоритм, основанный на учете уровневой стоимости литералов. Для каждого набора целей применение этой эвристики осуществляется в описанном ниже порядке. 1. Определить литерал с максимальной уровневой стоимостью. 2. Чтобы достичь этого литерала, выбрать в первую очередь действие с самыми легкими для выполнения предусловиями. Это означает, что действие нужно выбирать так, чтобы сумма (или максимум) уровневых стоимостей его предусловий была минимальной.
<< В начало < Предыдущая 1 2 3 4 Следующая > В конец >>
|